Todos los pronósticos son inexactos, esto puede sonar evidente, sin embargo de esa inexactitud  surge una idea muy importante: ¿cuán preciso es mi modelo? Es por ello que todas las métricas de calidad en el proceso de proyección de la demanda tienen como ingrediente principal el error. (Makridakis & Hyndman, 1998), (Vandeput, 2019). La diferencia entre los valores reales y los pronosticados da como resultado su valor numérico* e_t=R_t-P_t ¹  , el cual puede adoptar un signo negativo o positivo**.

e_t= Error del pronóstico para el periodo t. (1)
R_t = Observación real o Cantidad de Demanda Real para el periodo t.
P_t = Valor de Pronóstico o Cantidad de Demanda pronosticada para el periodo t.

*Algunos libros muestran éste cálculo a la inversa P - R y ese cambio no tienen ningún efecto sobre el resultado final de las métricas del error.

** Cuando la Cantidad Real Demandada (Rt)  es mayor que la Proyección de la Demanda, el signo del error es positivo y viceversa cuando es menor.

Dos dimensiones de la calidad

Existen dos dimensiones principales de la calidad de un pronóstico: el sesgo y la precisión (Hyndman & Athanasopoulos, 2014), para explicar de manera simplificada estos dos conceptos veamos la imagen a continuación: 

La precisión es la cercanía de las observaciones reales con relación al pronóstico que se tenía de ellas, y el sesgo es una tendencia persistente a pronosticar por encima o por debajo, por fuera, de las observaciones reales (Oliva & Watson, 2009; Vandeput, 2019).

Ninguna métrica hace un buen trabajo capturando ambas dimensiones de manera individual, así que vale la pena tener múltiples (las necesarias, sin embargo surge la pregunta: ¿cuál métrica utilizar?  

Midiendo el sesgo

Las dos métricas comúnmente utilizadas para medir el sesgo son la Desviación Media (MD) ⁽²⁾ Mean Deviation por sus siglas en inglés y el Error Porcentual Medio (MPE) ⁽³⁾ Mean Percentage Error.

Al utilizarlas, el sesgo queda en evidencia porque los signos de las magnitudes se contraponen entre sí, por lo tanto, nos permiten comprender si por un lado existe un exceso de predicciones positivas (por arriba) o negativas (por debajo) o bien el error medio oscila cercano al cero ya que cuanto más alejados de cero se encuentren los valores de la MD ⁽²⁾ o el porcentaje de la MPE ⁽³⁾, un problema de sesgo en el modelo de pronóstico será más evidente. El beneficio de medirlo utilizando la última está en su interpretación porcentual, lo que facilita la comparación entre distintos modelos y/o porciones de la demanda.

Midiendo la precisión

Para cuantificar la precisión hay que evitar la influencia de los signos en el cálculo, la Desviación Media Absoluta (MAD) ⁽⁴⁾ y El Error Cuadrático Medio (MSE) ⁽⁵⁾ cumplen esa función; su uso tiene sentido al presenciar mucha volatilidad en la demanda, en este caso se recomienda utilizar la MSE para tener la sensibilidad de captar esos saltos de valores. Un problema que encontraremos al utilizarla se dará al tratar de interpretar su valor, por este motivo, una métrica de fácil interpretación que logra “percibir” cambios fuertes es la Raíz del Error Cuadrático Medio (RMSE) ⁽⁶⁾ Root Mean Squared Error por sus siglas en inglés, es más “sensible” porque el error se eleva al cuadrado y sólo después de obtener el promedio se toma la raíz cuadrada con el fin de convertir la métrica a un valor entendible, es decir, expresado en unidades.

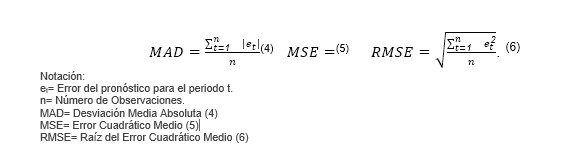
La gran utilidad de la RMSE ⁽⁶⁾, es su aplicación práctica, al ser utilizada en reemplazo de la desviación estándar, permite optimizar cálculos, tanto de pronóstico de la demanda, como de stock de seguridad, entre otras partes de la cadena de suministro. Esto se debe a que la RMSE ⁽⁶⁾ se calcula con la diferencia entre la observación real y el pronóstico (el error), mientras que la desviación estándar mide la dispersión de los datos alrededor de la media, es decir, en caso de usar siempre la media como pronóstico, ambos datos serían iguales. (“RMSE vs Standard deviation in population,” n.d.)

En el caso de tratar de comparar la dimensión de precisión de los pronósticos para diferentes modelos y/o porciones de la curva de demanda se recomienda utilizar también una métrica con valor porcentual como resultado, para ello podemos utilizar la Error Porcentual Absoluto Medio (MAPE - Mean Absolute Percent Error)⁽⁷⁾. Note que MAPE ⁽⁷⁾ y MPE⁽³⁾ son parecidas, con la diferencia que MAPE utiliza valores absolutos para evitar la influencia de los signos (sesgo) en el cálculo.

En la tabla a continuación se ejemplifica la forma de realizar el cálculo para cada una de las métricas aquí expuestas:

Aprende de tus errores

Es necesario aclarar que se debe aprender de los errores, y esta es posiblemente la razón más valiosa para utilizarlas, como bien lo explica Larry Lapide: “...Sin embargo, las métricas no agregan ningún valor si no se aprende nada de ellas, es decir, no se toma ninguna acción para mejorar el proceso. Un aporte significativo para este aprendizaje implica el análisis de las porciones de los datos en la que los pronósticos de demanda son más y menos precisos. Esto ayuda para evaluar cuáles métodos de pronóstico funcionan bien, o no, como también para ayudar a identificar áreas donde se deben alternar los métodos que pueden mejorar la precisión…” (Lapide 2007)

En resumen, independiente del método de pronóstico utilizado, se querrá medir la calidad, la cual tiene dos dimensiones principales: el sesgo y la precisión. Ninguna métrica individual hace un buen trabajo capturando ambas, así que vale la pena tener múltiples métricas, las necesarias. Entre las métricas más comunes para mostrar el sesgo, se utiliza la Desviación Media (MD) ⁽²⁾ y Error Porcentual Medio (MPE) ⁽³⁾. Para mostrar la precisión se usan el Error Porcentual Absoluto Medio (MAPE) ⁽⁵⁾ y Raíz del Error Cuadrático Medio (RMSE) ⁽⁶⁾, sin embargo, existen muchas variaciones utilizadas en la práctica. Estas métricas deben ser utilizadas para optimizar tanto la gestión de inventarios como la gestión de la demanda, e.g. Mejorando los cálculos de inventario reemplazando la desviación estándar por la RMSE; aprendiendo de ellas tomando acciones para mejorar el proceso de pronóstico subdividiendo los datos en partes y haciendo comparaciones de cómo se hubieran comportado diferentes modelos en ciertas porciones de la demanda donde el margen de error aumenta.

No existe una métrica ideal para todos los casos, como científicos de la cadena de suministro lo mejor es experimentar para conocer cuál es mejor en cada caso particular.

Fuentes de error en el pronóstico

Aquellos que desean reducir el error pueden encontrar una respuesta buscando en tres lugares:
1) Los datos que ingresan al modelo de pronóstico (Garbage in - Garbage out)
2) El modelo en sí mismo (Ejemplo: Usar suavizado exponencial Holt-Winter para demanda estacionaria)
3) El contexto del pronóstico (Espacio-Tiempo)

Espero que un gran error en sus pronósticos no se deba a una falta de esfuerzo. 

Hyndman, R. J., & Athanasopoulos, G. (2014). Forecasting: Principles and Practice. OTexts.Makridakis, S. G., & Hyndman, R. J. (1998). Forecasting: Methods and Applications. Wiley.Oliva, R., & Watson, N. (2009). Managing Functional Biases in Organizational Forecasts: A Case Study of Consensus Forecasting in Supply Chain Planning. International Journal of Operations & Production Management, 18(2), 138–151.RMSE vs Standard deviation in population. (n.d.). Retrieved November 7, 2019, from Cross Validated website: https://stats.stackexchange.com/questions/264906/rmse-vs-standard-deviation-in-populationVandeput, N. (2019, July 5). Forecast KPI: RMSE, MAE, MAPE & Bias. Retrieved October 31, 2019, from Medium website: https://medium.com/analytics-vidhya/forecast-kpi-rmse-mae-mape-bias-cdc5703d242dFragments from Key-concepts document and others documents from MITx MicroMasters in Supply Chain Management MIT Center for Transportation & Logistics・Cambridge, MA 02142 USA ・scm_mm@mit.edu This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

Leonardo Garcia Razera 

Supply Chain Management Micromaster - Massachusetts Institute of Technology trough Edx 

Maestrando en Comercio Internacional - UAGRM Business School

Administrador de Empresas - UAGRM

Co-Founder and Consultant at Heuristica.biz (Bolivia)

leonardo@heuristica.biz   

+591 75017687